Tree Design
Overview
The tree-based container has the following declaration:
template<
typename Key,
typename Mapped,
typename Cmp_Fn = std::less<Key>,
typename Tag = rb_tree_tag,
template<
typename Const_Node_Iterator,
typename Node_Iterator,
typename Cmp_Fn_,
typename Allocator_>
class Node_Update = null_tree_node_update,
typename Allocator = std::allocator<char> >
class tree;
The parameters have the following meaning:
- Key is the key type.
- Mapped is the mapped-policy.
- Cmp_Fn is a key comparison functor
- Tag specifies which underlying data structure to use.
- Node_Update is a policy for updating node invariants. This is described in Node Invariants.
- Allocator is an allocator type.
The Tag parameter specifies which underlying data structure to use. Instantiating it by rb_tree_tag, splay_tree_tag, or ov_tree_tag, specifies an underlying red-black tree, splay tree, or ordered-vector tree, respectively; any other tag is illegal. Note that containers based on the former two contain more types and methods than the latter (e.g., reverse_iterator and rbegin), and different exception and invalidation guarantees.
Node Invariants
Consider the two trees in Figures Some node invariants A and B. The first is a tree of floats; the second is a tree of pairs, each signifying a geometric line interval. Each element in a tree is refered to as a node of the tree. Of course, each of these trees can support the usual queries: the first can easily search for 0.4; the second can easily search for std::make_pair(10, 41).
Each of these trees can efficiently support other queries. The first can efficiently determine that the 2rd key in the tree is 0.3; the second can efficiently determine whether any of its intervals overlaps std::make_pair(29,42) (useful in geometric applications or distributed file systems with leases, for example). (See tree_order_statistics.cc and tree_intervals.cc for examples.) It should be noted that an std::set can only solve these types of problems with linear complexity.
In order to do so, each tree stores some metadata in each node, and maintains node invariants clrs2001]. The first stores in each node the size of the sub-tree rooted at the node; the second stores at each node the maximal endpoint of the intervals at the sub-tree rooted at the node.
Some node invariants.
Supporting such trees is difficult for a number of reasons:
- There must be a way to specify what a node's metadata should be (if any).
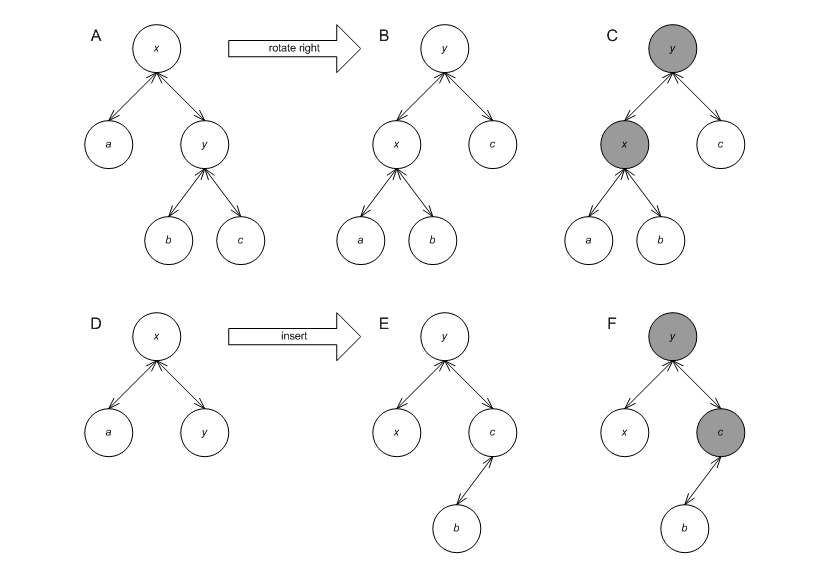
- Various operations can invalidate node invariants. E.g., Figure Invalidation of node invariants shows how a right rotation, performed on A, results in B, with nodes x and y having corrupted invariants (the grayed nodes in C); Figure Invalidation of node invariants shows how an insert, performed on D, results in E, with nodes x and y having corrupted invariants (the grayed nodes in F). It is not feasible to know outside the tree the effect of an operation on the nodes of the tree.
- The search paths of standard associative containers are defined by comparisons between keys, and not through metadata.
- It is not feasible to know in advance which methods trees can support. Besides the usual find method, the first tree can support a find_by_order method, while the second can support an overlaps method.
Invalidation of node invariants.
These problems are solved by a combination of two means: node iterators, and template-template node updater parameters.
Node Iterators
Each tree-based container defines two additional iterator types, const_node_iterator and node_iterator. These iterators allow descending from a node to one of its children. Node iterator allow search paths different than those determined by the comparison functor. tree supports the methods:
const_node_iterator
node_begin() const;
node_iterator
node_begin();
const_node_iterator
node_end() const;
node_iterator
node_end();
The first pairs return node iterators corresponding to the root node of the tree; the latter pair returns node iterators corresponding to a just-after-leaf node.
Node Updater (Template-Template) Parameters
The tree-based containers are parametrized by a Node_Update template-template parameter. A tree-based container instantiates Node_Update to some node_update class, and publicly subclasses node_update. Figure A tree and its update policy shows this scheme, as well as some predefined policies (which are explained below).
A tree and its update policy.
node_update (an instantiation of Node_Update) must define metadata_type as the type of metadata it requires. For order statistics, e.g., metadata_type might be size_t. The tree defines within each node a metadata_type object.
node_update must also define the following method for restoring node invariants:
void
operator()(node_iterator nd_it, const_node_iterator end_nd_it)
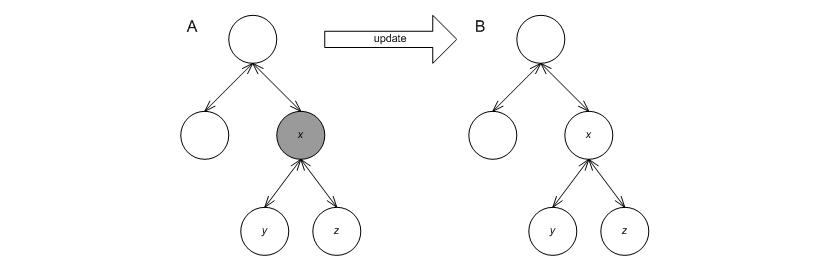
In this method, nd_it is a node_iterator corresponding to a node whose A) all descendants have valid invariants, and B) its own invariants might be violated; end_nd_it is a const_node_iterator corresponding to a just-after-leaf node. This method should correct the node invariants of the node pointed to by nd_it. For example, say node x in Figure Restoring node invariants-A has an invalid invariant, but its' children, y and z have valid invariants. After the invocation, all three nodes should have valid invariants, as in Figure Restoring node invariants-B.
Invalidation of node invariants.
When a tree operation might invalidate some node invariant, it invokes this method in its node_update base to restore the invariant. For example, Figure Insert update sequence diagram shows an insert operation (point A); the tree performs some operations, and calls the update functor three times (points B, C, and D). (It is well known that any insert, erase, split or join, can restore all node invariants by a small number of node invariant updates [clrs2001].)
Insert update sequence diagram.
To complete the description of the scheme, three questions need to be answered:
- How can a tree which supports order statistics define a method such as find_by_order?
- How can the node updater base access methods of the tree?
- How can the following cyclic dependency be resolved? node_update is a base class of the tree, yet it uses node iterators defined in the tree (its child).
The first two questions are answered by the fact that node_update (an instantiation of Node_Update) is a public base class of the tree. Consequently:
- Any public methods of node_update are automatically methods of the tree [alexandrescu01modern]. Thus an order-statistics node updater, tree_order_statistics_node_update defines the find_by_order method; any tree instantiated by this policy consequently supports this method as well.
- In C++, if a base class declares a method as virtual, it is virtual in its subclasses. If node_update needs to access one of the tree's methods, say the member function end, it simply declares that method as virtual abstract.
The cyclic dependency is solved through template-template parameters. Node_Update is parametrized by the tree's node iterators, its comparison functor, and its allocator type. Thus, instantiations of Node_Update have all information required.
pb_ds assumes that constructing a metadata object and modifying it are exception free. Suppose that during some method, say insert, a metadata-related operation (e.g., changing the value of a metadata) throws an exception. Ack! Rolling back the method is unusually complex.
In Interface::Concepts::Null Policy Classes a distinction was made between redundant policies and null policies. Node invariants show a case where null policies are required.
Assume a regular tree is required, one which need not support order statistics or interval overlap queries. Seemingly, in this case a redundant policy - a policy which doesn't affect nodes' contents would suffice. This, would lead to the following drawbacks:
- Each node would carry a useless metadata object, wasting space.
- The tree cannot know if its Node_Update policy actually modifies a node's metadata (this is halting reducible). In Figure Useless update path , assume the shaded node is inserted. The tree would have to traverse the useless path shown to the root, applying redundant updates all the way.
Useless update path.
A null policy class, null_tree_node_update solves both these problems. The tree detects that node invariants are irrelevant, and defines all accordingly.
Additional Methods
Tree-based containers support split and join methods. It is possible to split a tree so that it passes all nodes with keys larger than a given key to a different tree. These methods have the following advantages over the alternative of externally inserting to the destination tree and erasing from the source tree:
- These methods are efficient - red-black trees are split and joined in poly-logarithmic complexity; ordered-vector trees are split and joined at linear complexity. The alternatives have super-linear complexity.
- Aside from orders of growth, these operations perform few allocations and de-allocations. For red-black trees, allocations are not performed, and the methods are exception-free.